じゃんけん判定を例にして、アルゴリズムの取り出しについて考えます。

じゃんけんはコンピュータとは無縁の作業ですが、この作業をコンピュータで扱うには、じゃんけん動作をコンピュータが扱うことができるデータや処理に対応づける必要があります。

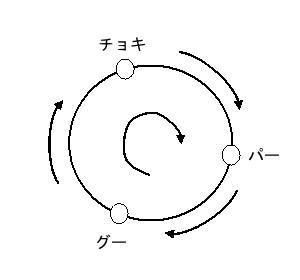
まず、グー、チョキ、パーにそれぞれ数値の0、1、2を対応づけます。グー、チョキ、パーの勝ちの順に並べると、0→1→2になります。これは、2→0→1でも、1→2→0の順でもかまいません。

じゃんけんは三すくみになっていて、下の図のように、右回りに考えると、手前の手が次の手に”勝ち”となります。しかし、次の次の手には”負け”となります。

Aさん、Bさんの手（0、1、2のいずれか1つ）を、それぞれ変数XA、XBが保有するとします。このとき、次が成り立ちます。

　　　　　　　　　　（Aさんの結果）
XA＝XB　　　　　　⇒　　相子
(XA+1)mod(3)=XB　　⇒　　勝ち
(XA+2)mod(3)=XB　　⇒　　負け

これは、三すくみの考え方から明らかです。

これは一般に知られた判定法：

　　　　　　　　　　（Aさんの結果）
(XA-XB+3)mod(3)=0　⇒　　相子
(XA-XB+3)mod(3)=1　⇒　　負け
(XA-XB+3)mod(3)=2　⇒　　勝ち

と同等です。それはmodの加減乗算の定理を用いて証明できます。

２つの判定法で使われている式はそのままほとんどのプログラミング言語で表現できます。

このようにして、コンピュータとは無縁なじゃんけんという作業をコンピュータで扱うことが可能となります。